[ITEM]

 [/ITEM]
[/ITEM]
12.01.2019
97


Contoh soal cerita fungsi komposisi dan jawaban. Contoh soal: Apabila x, y anggota Kumpulan Soal Cerita Program Linear September 8th 2013 soal-soal Contoh Soal Deret Geometri dan Fungsi. Grafik fungsi dan fungsi linear y.
Sistem Pertidaksamaan Linear Pertidaksamaan linear merupakan sebuah pertidaksamaan dengan kombinasi operasi antar variabel yang ditandai dengan tanda (kurang dari), (kurang dari sama dengan), (lebih dari), atau (lebih dari sama dengan). Sedangkan gabungan dari beberapa pertidaksamaan linear disebut sistem pertidaksamaan linear. Sistem pertidaksamaan linear pada program linear yang diajarkan di tingkat SMA biasanya melibatkan dua variabel dengan dua atau lebih pertidaksamaan linear. Bagian ini menjadi dasar untuk dapat menyelesaikan masalah terkait program linear. Salah satu langkah penting dalam sistem pertidaksamaan linear pada pembahasan tentang program linear adalah dapat secara tepat menggambarkan garis dan daerah yang memenuhi di bidang kartesius. Pada bagian ini, sobat akan mempelajari bagaimana cara menentukan dua langkah tersebut.
Sebelumnya, ingat kembali sistem pertidaksamaan linear yang akan diberikan pada contoh di bawah. Contoh sistem pertidaksamaan linear Cara menggambar persamaan garis lurus dan menentukan daerah yang memenuhi: Himpunan penyelesaian suatu pertidaksamaan linear dua peubah dapat ditentukan dengan cara sebagai berikut. • Gambarlah garis pada bidang kartesius, cara lebih lengkapnya dapat dilihat.
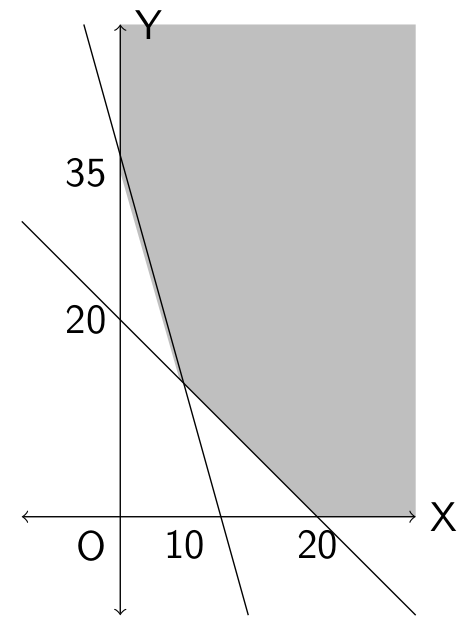
• Ambil sembarang titik di luar garis kemudian hitung nilai dan bandingkan dengan nilai c. • Jika maka daerah yang memuat adalah daerah penyelesaian dari pertidaksamaan. • Jika maka daerah yang memuat adalah daerah penyelesaian dari pertidaksamaan. Contoh cara menentukan daerah himpunan penyelesaian dari sistem pertidaksamaan linear dua peubah. Diberikan sistem pertidaksamaan linear berikut. Cari tahu daerah yang memenuhi sistem pertidaksamaan linear di atas.
Khuda jaane mp3 pk song download. • Daerah yang memenuhi pertidaksamaan. • Daerah yang memenuhi pertidaksamaan.
• Daerah yang memenuhi gabungan dari empat sistem pertidaksamaan linear:,,, dan. Model Matematika Model soal yang diberikan pada program linear biasanya berupa soal cerita.
Agar dapat menyelesaikan soal cerita yang diberikan, sobat idschool perlu merubahnya ke dalam model matematika. Model matematika merupakan suatu cara merubah permasalahan sehari-hari ke dalam bahasa matematika dalam bentuk persamaan, pertidaksamaan, dan fungsi. Untuk penjelasan lebih detailnya, perhatikan penyelesaian kasus berikut. Contoh soal model matematika Tentukan model matematika dari soal di bawah. Sebuah adonan roti basah dibuat dengan 2 kg tepung dan 1 kg gula. Sedangkan sebuah adonan roti kering dibuat menggunakan 2 kg tepung dan 3 kg gula. Ibu memiliki persediaan tepung sebanyak 6 kg dan gula sebanyak 5 kg.

Jika setiap satu adonan kue basah dapat memberikan untung Rp75.000,00 dan setiap adonan kue kering dapat memberikan untung Rp60.000,00, berapakah banyak kombinasi adonan roti yang dapat dibuat untuk mendapatkan keuntungan maksimal? Pembahasan: Misalkan: x = adonan roti basah y = adonan roti kering Perhatikan tabel di bawah. Sehingga diperoleh model matematika dari soal di atas adalah seperti berikut. Pembahasan yang diberikan hanya berhenti sampai di sini, belum sampai menentukan kombinasi jenis roti yang dibuat untuk mendapatkan keuntungan maksimal. Solusi selanjutnya akan dibahas pada penjabaran materi di bawah.
Cara Menyelesaikan Masalah Program Linear Cara menyelesaikan masalah program linear dapat dikatakan sebagai proses untuk menentukan nilai optimum dari suatu pertidaksamaan. Nilai tersebut dapat berupa nilai maksimum atau minimum, tergantung dari soal yang diberikan. Bentuk umum fungsi objektif dari suatu model matematika adalah.
Terdapat dua metode yang dapat digunakan untuk menentukan nilai optimum tersebut, yaitu metode uji titik pojok dan garis selidik. Penjabaran secara lebih jelasnya dapat dilihat pada pembahasan di bawah.
Metode Uji Titik Pojok Sesuai namanya, metode uji titik pojok dilakukan dengan menghitung nilai fungsi tujuan dari titik pojok yang diperoleh. Titik pojok yang dimaksud di sini adalah titik-titik koordinat yang membatasi daerah layak dari suatu sistem pertidaksamaan linear. Langkah – langkah yang dilakukan untuk menentukan nilai optimum dengan metode uji titik pojok adalah sebagai berikut. • Menentukan garis-garis sistem pertidaksamaan yang menjadi fungsi kendala dari persoalan yang diberikan. • Menentukan titik-titik pojok yang merupakan koordinat pembatas daerah yang memenuhi fungsi kendala. • Menghitung nilai optimum dari titik-titik pojok yang diperoleh. • Mendapatkan nilai maksimum atau minimum sesuai permasalahan.
Untuk memperjelas pemahaman materi tentang mencari nilai optimum dengan metode uji titik pojok, kita akan menyelesaikan permasalah yang telah dibahas sebagian pada bagian model matematika. Berdasarkan pembahasan sebelumnya diperoleh sistem pertidaksamaan berikut. Lihat kembali soal yang diberikan, fungsi tujuan dapat diperoleh dari kalimat berikut. Jika setiap satu adonan kue basah dapat memberikan untung Rp75.000,00 dan setiap adonan kue kering dapat memberikan untung Rp60.000,00. Jadi, fungsi tujuannya adalah memaksimalkan. Menggambar daerah yang memenuhi sistem pertidaksamaan di atas. Menentukan titik koordinat yang mennjadi titik pojok pembatas daerah layak dari permasalahan sistem pertidaksamaan.
- Author: admin
- Category: Category
Search
Most Viewed Pages
- Acer Aspire V5-431 Device Manage Bluetooth Masalah Tak Boleh
- Neraca Laba Rugi Perusahaan Kontraktor
- Sony Drivers Update Utility For Windows 7 Cracked Background
- Situs Download Film Semi Korea
- Nonton Online Anime Cooking Master Boy Sison 2
- Bukan Maksudku Melukaimu Mp3
- 50shades Of Grey Full Movie Download In Hindi

Contoh soal cerita fungsi komposisi dan jawaban. Contoh soal: Apabila x, y anggota Kumpulan Soal Cerita Program Linear September 8th 2013 soal-soal Contoh Soal Deret Geometri dan Fungsi. Grafik fungsi dan fungsi linear y.
Sistem Pertidaksamaan Linear Pertidaksamaan linear merupakan sebuah pertidaksamaan dengan kombinasi operasi antar variabel yang ditandai dengan tanda (kurang dari), (kurang dari sama dengan), (lebih dari), atau (lebih dari sama dengan). Sedangkan gabungan dari beberapa pertidaksamaan linear disebut sistem pertidaksamaan linear. Sistem pertidaksamaan linear pada program linear yang diajarkan di tingkat SMA biasanya melibatkan dua variabel dengan dua atau lebih pertidaksamaan linear. Bagian ini menjadi dasar untuk dapat menyelesaikan masalah terkait program linear. Salah satu langkah penting dalam sistem pertidaksamaan linear pada pembahasan tentang program linear adalah dapat secara tepat menggambarkan garis dan daerah yang memenuhi di bidang kartesius. Pada bagian ini, sobat akan mempelajari bagaimana cara menentukan dua langkah tersebut.
Sebelumnya, ingat kembali sistem pertidaksamaan linear yang akan diberikan pada contoh di bawah. Contoh sistem pertidaksamaan linear Cara menggambar persamaan garis lurus dan menentukan daerah yang memenuhi: Himpunan penyelesaian suatu pertidaksamaan linear dua peubah dapat ditentukan dengan cara sebagai berikut. • Gambarlah garis pada bidang kartesius, cara lebih lengkapnya dapat dilihat.
• Ambil sembarang titik di luar garis kemudian hitung nilai dan bandingkan dengan nilai c. • Jika maka daerah yang memuat adalah daerah penyelesaian dari pertidaksamaan. • Jika maka daerah yang memuat adalah daerah penyelesaian dari pertidaksamaan. Contoh cara menentukan daerah himpunan penyelesaian dari sistem pertidaksamaan linear dua peubah. Diberikan sistem pertidaksamaan linear berikut. Cari tahu daerah yang memenuhi sistem pertidaksamaan linear di atas.
Khuda jaane mp3 pk song download. • Daerah yang memenuhi pertidaksamaan. • Daerah yang memenuhi pertidaksamaan.
• Daerah yang memenuhi gabungan dari empat sistem pertidaksamaan linear:,,, dan. Model Matematika Model soal yang diberikan pada program linear biasanya berupa soal cerita.
Agar dapat menyelesaikan soal cerita yang diberikan, sobat idschool perlu merubahnya ke dalam model matematika. Model matematika merupakan suatu cara merubah permasalahan sehari-hari ke dalam bahasa matematika dalam bentuk persamaan, pertidaksamaan, dan fungsi. Untuk penjelasan lebih detailnya, perhatikan penyelesaian kasus berikut. Contoh soal model matematika Tentukan model matematika dari soal di bawah. Sebuah adonan roti basah dibuat dengan 2 kg tepung dan 1 kg gula. Sedangkan sebuah adonan roti kering dibuat menggunakan 2 kg tepung dan 3 kg gula. Ibu memiliki persediaan tepung sebanyak 6 kg dan gula sebanyak 5 kg.

Jika setiap satu adonan kue basah dapat memberikan untung Rp75.000,00 dan setiap adonan kue kering dapat memberikan untung Rp60.000,00, berapakah banyak kombinasi adonan roti yang dapat dibuat untuk mendapatkan keuntungan maksimal? Pembahasan: Misalkan: x = adonan roti basah y = adonan roti kering Perhatikan tabel di bawah. Sehingga diperoleh model matematika dari soal di atas adalah seperti berikut. Pembahasan yang diberikan hanya berhenti sampai di sini, belum sampai menentukan kombinasi jenis roti yang dibuat untuk mendapatkan keuntungan maksimal. Solusi selanjutnya akan dibahas pada penjabaran materi di bawah.
Cara Menyelesaikan Masalah Program Linear Cara menyelesaikan masalah program linear dapat dikatakan sebagai proses untuk menentukan nilai optimum dari suatu pertidaksamaan. Nilai tersebut dapat berupa nilai maksimum atau minimum, tergantung dari soal yang diberikan. Bentuk umum fungsi objektif dari suatu model matematika adalah.
Terdapat dua metode yang dapat digunakan untuk menentukan nilai optimum tersebut, yaitu metode uji titik pojok dan garis selidik. Penjabaran secara lebih jelasnya dapat dilihat pada pembahasan di bawah.
Metode Uji Titik Pojok Sesuai namanya, metode uji titik pojok dilakukan dengan menghitung nilai fungsi tujuan dari titik pojok yang diperoleh. Titik pojok yang dimaksud di sini adalah titik-titik koordinat yang membatasi daerah layak dari suatu sistem pertidaksamaan linear. Langkah – langkah yang dilakukan untuk menentukan nilai optimum dengan metode uji titik pojok adalah sebagai berikut. • Menentukan garis-garis sistem pertidaksamaan yang menjadi fungsi kendala dari persoalan yang diberikan. • Menentukan titik-titik pojok yang merupakan koordinat pembatas daerah yang memenuhi fungsi kendala. • Menghitung nilai optimum dari titik-titik pojok yang diperoleh. • Mendapatkan nilai maksimum atau minimum sesuai permasalahan.
Untuk memperjelas pemahaman materi tentang mencari nilai optimum dengan metode uji titik pojok, kita akan menyelesaikan permasalah yang telah dibahas sebagian pada bagian model matematika. Berdasarkan pembahasan sebelumnya diperoleh sistem pertidaksamaan berikut. Lihat kembali soal yang diberikan, fungsi tujuan dapat diperoleh dari kalimat berikut. Jika setiap satu adonan kue basah dapat memberikan untung Rp75.000,00 dan setiap adonan kue kering dapat memberikan untung Rp60.000,00. Jadi, fungsi tujuannya adalah memaksimalkan. Menggambar daerah yang memenuhi sistem pertidaksamaan di atas. Menentukan titik koordinat yang mennjadi titik pojok pembatas daerah layak dari permasalahan sistem pertidaksamaan.
Search
Most Viewed Pages
- Acer Aspire V5-431 Device Manage Bluetooth Masalah Tak Boleh
- Neraca Laba Rugi Perusahaan Kontraktor
- Sony Drivers Update Utility For Windows 7 Cracked Background
- Situs Download Film Semi Korea
- Nonton Online Anime Cooking Master Boy Sison 2
- Bukan Maksudku Melukaimu Mp3
- 50shades Of Grey Full Movie Download In Hindi